Write out the function given in the question
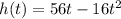
Note that at the maximum height the derivative of the function would be equal to zero
Find the derivative of the function using the formula
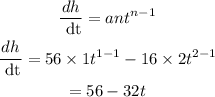
Equate the derivative to zero to get the value of t because the derivative is zero at maximum height
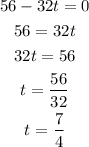
Substitute the value of t into the function
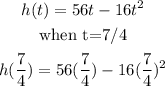
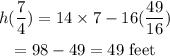
Hence, the maximum height that the ball will reach is 49feet