SOLUTION
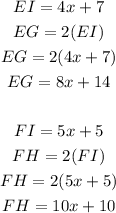
To find x, equate both diagonals FH and EG as they are equal
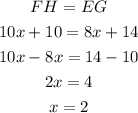
To find EG
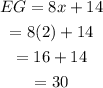
EG = 30
Since lenght IE and IH are equal (15) , triangle IHE is an iscoceless triangle
with equal base angles
x+x+54=180
2x+54=180
2x=180-54
2x=126
x=126/2
x=63degrees.
[tex]\begin{gathered} \text{Therefore} \\