Let the speed of Boat is B and speed of stream is S
The expression for Speed is :
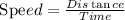
Time taken by the boat to travel 24 miles downstream is 2 hours
So, speed of boat in downtsream :
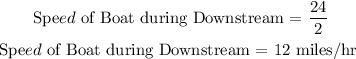
Time taken by the boat tp travel 24 miles upstream is 4 hours

Downstream means : A boat is said to go downstream if it is moving along the direction of the stream i.e net speed is the sum of speed of boat + Speed of river
From the data :
Speed of Boat + Speed of stream = 12
B + S = 12 (1)
Upstream Means : If the boat is flowing in the opposite direction to the stream, it is called upstream.i.e. the net speed is the difference of speed of baot and river
From the given data : Speed of Boat - Speed of stream = 6
B - S = 6 (2)
Simplify the equation (1) & (2)
B + S = 12
B - S = 6
Add the equations :
B + S + B - S = 12 + 6
2B = 18
B = 18/2
B = 9
i.e. Speed of Boat is 9 miles/hr
Substitute B = 9 in the equation (1)
B + S = 12
9 + S = 12
S = 12 - 9
S = 3 miles/hr
Speed of stream of current water is 3 miles/hr
Answer : Speed of boat in still water is 9 miles/hr
speed of the current of the river is 3 miles/hr