Question

Topic quadratic graphfrom the table answer each carefully from the graph

Answer 1

The graph is concave down.

y-intercept: (0, 6)

(i). x = -3 and x = 2.

Step-by-step explanation:

Plotting the function gives us information about the x- and the y-intercepts.

(ii). The x - intercepts of f(x) are solutions to

`-x+6-x^2=0`

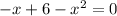
The above equation is a quadratic equation, and therefore, can be solve using the quadratic formula.

Now, the quadratic formula says that if we have a quadratic equation of the form

`ax^2+bx+c=0`

the solution is given by

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Now in our case, we have

`-x^2-x+6=0`

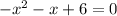
Therefore, for the quadratic formula, we have a = -1, b = -1, and c = 6; therefore,

`x=\frac{-(-1)_{}\pm\sqrt[]{(-1)^2-4(-1)(6)}}{2(-1)}`
`\Rightarrow x=\frac{1_{}\pm\sqrt[]{25}}{-2}`
`x=-(1\pm5)/(2)`
`\begin{gathered} x=-(1-5)/(2)=2 \\ x=-(1+5)/(2)=-3 \\ \end{gathered}`

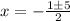
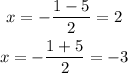
Therefore, we see that the solutions to our quadratic equation ( and therefore, the x-intercepts of f(x)) are x = 2 and x = -3.