We have to calculate the perimeter of this composite figure.
This perimeter will be composed by different segments:
0. One length of the rectangle (21 ft)
,
1. One width of the rectangle (14 ft)
,
2. Another lwngth of the rectangle (21 ft), and
,
3. A semicircle (yet to be calculated).
We can calculate the length of the semicircle as half the perimeter of a circle. The diameter in this case is the width of the rectangle (14 ft).
Then, we can write:
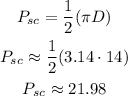
Then, we can now calculate the perimeter as the sum of the lengths of the segments we have listed:
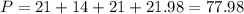
Answer: 77.98 ft of fence are required.