Given:
The points of the exponential function are (1,12) and (-1,0.75).
The objective is to write the equation of the exponential function.
Step-by-step explanation:
The general equation of exponential is,

First, substitute (1,12) in equation (1).
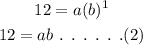
Now, substitute (-1,0.75) in equation (1).
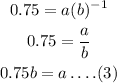
To find b:
Substitute the value of an in equation (2).
![\begin{gathered} 12=(0.75b)(b) \\ (12)/(0.75)=b^2 \\ 16=b^2 \\ \sqrt[]{16}=b \\ b=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/s4tev13wuhkdffolhpbluwi90b4s6df6zl.png)
To find a:
Substitute the value of b in equation (3),
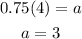
To find the equation:
Substitute the value of a and b in equation (1).

Hence, the equation of the exponential function is y = 3(4)^x.e