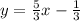For this case we need to remember the definition of a line given by this formula:

And we have the following points given: (2,3) and (5,8)
And we can find the slope with the following formula:
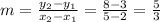
And using one point we got:
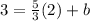
And solving for b we got:

And our equation would be: