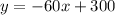ANSWER:

Explanation:
We have that the equation in its slope and intercept form is the following:
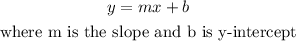
We calculate the slope as follows:

We calculate the slope for the computer value and for the printer value:
In the computer value, we have the points (0, 960) and (3, 405), replacing:
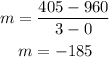
In the printer value, we have the points (0, 300) and (3, 120), replacing:
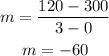
The intercept with b is the point when x is equal to 0, therefore, the two equations would be:
The equation for the value of computer:
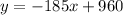
The equation for the value of printer: