Question

Please help me on this question (answer all parts please)

Answer 1

Case: Volume of Sphere

Method:

a) The volume of a sphere whose diameter, d= 28in

The radius,

r= 28/2

r= 14 in

The Volume, therefore:

`\begin{gathered} V=(4)/(3)\pi r^3 \\ V=(4)/(3)\pi*14*14*14 \\ V=11494.04\text{ }cubic\text{ }inches \end{gathered}`

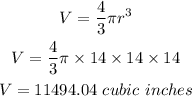
b) When half of the volume is used,

`\begin{gathered} V=(1)/(2)V_0 \\ V=(1)/(2)*11494.04 \\ V=5747.02\text{ }cubic\text{ }inches \end{gathered}`

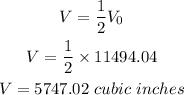
c) The radius of the halved volume

`\begin{gathered} V=(4)/(3)\pi r^3 \\ 5747.02=(4)/(3)\pi r^3 \\ r^3=(3*5747.02)/(4\pi) \\ r^3=1372 \\ r=\sqrt[3]{1372} \\ r=11.11\text{ }inches \end{gathered}`

Final answer: (To 2 d.p)

a) 11494.04 cubic inches

b) 5747.02 cubic inches

c) 11.11 inches