Question

Consider the line 8x+9y=2What is the slope of a line perpendicular to this line?What is the slope of a line parallel to this line?

Answer 1

Answer:

The slope of a line perpendicular to this line is 9/8

The slope of a line parallel to this line is -8/9

Step-by-step explanation:

Given:

8x + 9y = 2

To find:

a) The slope of the line perpendicular to the given line

b) The slope of the line parallel to the given line

a) To determine the line perpendicular to 8x + 9y = 2, we need to first find its slope

`\begin{gathered} \text{8x + 9y = 2} \\ 9y\text{ = 2 - 8x} \\ y\text{ = }(2-8x)/(9) \\ y\text{ = }(2)/(9)\text{ - }(8)/(9)x \\ \\ In\text{ equation of line: y = mx + b} \\ m\text{ = slope, b = y-intercept} \\ \\ slope\text{ = -8/9} \end{gathered}`

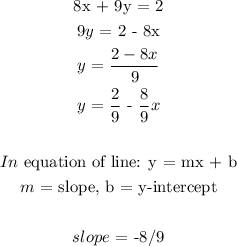
For two lines to be perpendicular, the slope of one line will be the negative reciprocal of the second line

slope of the 1st line = -8/9

reciprocal of the line = -(9/8) = -9/8

negative reciprocal = -(-9/8) = 9/8

This means the second line will have a slope of 9/8

The slope of a line perpendicular to this line is 9/8

b) For two lines to be parallel, the slope of both lines will be the same.

Since slope of the first is -8/9. The slope of the second line will also be -8/9

The slope of a line parallel to this line is -8/9