..
Given
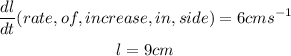
To Determine: The rate of increase in volume
The volume of a cube is given as
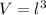
The rate of change of volume with respect to the length is the derivative of the volume function. So the derivative is as calculated below
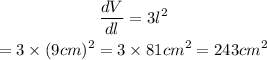
The rate of increase in volume would be
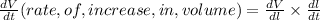
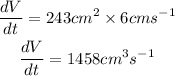
Hence, the rate of increase in volume is 1458cm³ per seconds