Question

The difference of two numbers is 4. If the sum of the smaller number and the square of the larger number is 86, what is the larger number?

Answer 1

The larger number could be 9 or -10.

Explanation:

Hi there!

Let the larger number be equal to a.

Let the smaller number to be equal to b.

We're given that their difference is 4:

`a-b=4`

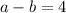
We're also given that the sum of the smaller number and the square of the larger number is 86:

`b+a^2=86`

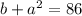
Rearrange the first equation to isolate a:

`a=4+b`

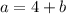
Substitute the first equation into the second:

`b+(4+b)^2=86\\b+(16+8b+b^2)=86\\b+16+8b+b^2=86\\16+9b+b^2=86\\b^2+9b-70=0`

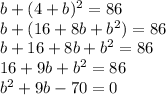
Factor:

`b^2+14b-5b-70=0\\b(b+14)-5(b+14)=0\\(b-5)(b+14)=0`

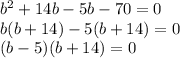
The zero-product property tells us that when multiple terms have a product of 0, then at least one of the terms is equal to 0:

`b-5=0\\b=5`

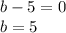
Or

`b+14=0\\b=-14`

Therefore, b, or the smaller number, could be either 5 or -14.

Now, use b to solve for a:

`a-5=4\\a=9`

Therefore, the larger number is 9 if the smaller number is 5.

`a+14=4\\a=-10`

Therefore, the larger number is -10 if the smaller number is -14.

I hope this helps!