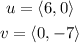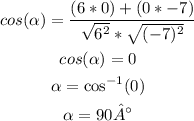Question

Find the angle (in radians) between the vectors. (Round your answer to two decimal places.)

Answer 1

`\alpha=90°`

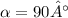
Explanation:

As a first step calculate the dot product of the vectors, the dot product is defined as the product of the magnitudes of the vectors multiplied by the cosine of the angle between them:

`a\cdot b=\lvert{a}\rvert *\lvert{b}\rvert *cos(\alpha)`

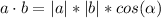
Now, make the angle the subject of the equation:

`cos(\alpha)=\frac{a\cdot b}{\lvert{a}\rvert *\lvert{b}\rvert}`

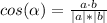
Remember that the magnitude is the square root of the sum of the vector's components to the second power. Hence, for the angle between the vectors:

`\begin{gathered} u=\langle6,0\rangle \\ v=\langle0,-7\rangle \end{gathered}`
`\begin{gathered} cos(\alpha)=((6*0)+(0*-7))/(√(6^2)*√((-7)^2)) \\ cos(\alpha)=0 \\ \alpha=\cos^(-1)(0) \\ \alpha=90° \end{gathered}`