SOLUTION
From the question, let the
Length of pine boards be represented as x and
Let the length of galvanized steel fencing be represented as y.
The diagram of Lucy Dog Daycare can be represented as follows
So, the Total cost C should include cost of two pine boards 2x and cost of one galvanized steel y. So we have
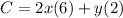
So, we have
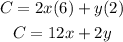
Also the total area is 800 square. That is
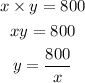
Now substituting the value of y into the cost equation, we have

Taking the derivative, we have

At minimum or maximum cost, the derivative should be equal to zero,
So
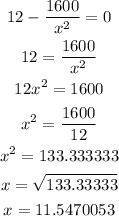
Hence x = 11.55 ft
From the equation above, where y was made the subject, we have

Hence y = 69.28 ft
Hence the dimensions that could be used at a minimum cost is 11.55 ft of pine boards by 69.28 ft of galvanized steel