Question

can anavar we're arguing about how to find the area of the composite figure below they both saw different shades of they both can be correct Which shapes do you see what is the composite area this figure which shapes do you see Jesus shapes to find the composite area

Answer 1

The composite figure is made by: 2 right triangles and 1 semicircle. Or 1 triangle and 1 semicircle. With any of the two combinations of shapes the area is the same.

To find the area you sum the area of each shape that compose the figure:

1 triangle and 1 semicircle:

`\begin{gathered} A=A_(\Delta)+A_s \\ \\ A=(1)/(2)b\cdot h+(1)/(2)\pi\cdot r^2 \end{gathered}`

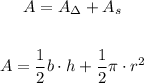
As the given figure has the diameter of the circle you find the radius as follow:

`\begin{gathered} r=(d)/(2) \\ r=(14m)/(2) \\ r=7m \end{gathered}`

The base of the triangle is 14m and the height is 10m.

`\begin{gathered} A=(1)/(2)(14m)(10m)+(1)/(2)\pi(7m)^2 \\ \\ A=(140)/(2)m^2+(49\pi)/(2)m^2 \\ \\ A=70m^2+76.97m^2 \\ \\ A=146.97m^2 \end{gathered}`

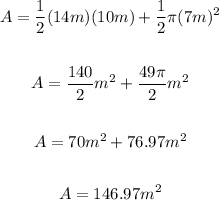
The area of the composite figure is 146.97 square meters