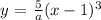Question

Suppose the graph of a cubie polnemial functionhas the same zeroes and passes through thecoordinate (0,-5)Describe the steps for writing the equation of thiscubie polynomial function

Answer 1

Step 1: Write the general form of a cubic equation having the same zeros

A cubic function having the same zeros take the form:

`y=k(x-a)^3`

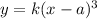
Step 2: Find the constant, k

Since the graph passes through the point (0, -5), substitute x = 0 and y = -5 into the general equation to find the constant, k.

`\begin{gathered} -5=k(0-a)^3 \\ -5=k(-a)^3 \\ -5=-ka^3 \\ k\text{ = }(-5)/(-a^3) \\ k\text{ = }(5)/(a^3) \end{gathered}`

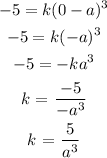
Step 3: Substitute the value of k into the general equation to find the equation for the cubic polynomial function

`\begin{gathered} y\text{ = }(5)/(a^3)(x-a)^3 \\ y\text{ = }(5(x-a)^3)/(a^3) \\ y\text{ = 5(}(x-a)/(a))^3 \\ y\text{ = 5(}(x)/(a)-(a)/(a))^3 \\ y\text{ = 5(}(x)/(a)-1)^3 \end{gathered}`

The equation for the cubic polynomial function is therefore:

`y\text{ = }(5)/(a)(x-1)^3`