Question

The Pear company sells pPhones. The cost to manufacture 2 pPhones isC(x) 19x² + 61000x + 18324 dollars (this includes overhead costs and production costs for eachpPhone). If the company sells 2 pPhones for the maximum price they can fetch, the revenue function willbe R(x) = - 23x² + 1490002 dollars.How many pPhones should the Pear company produce and sell to maximimze profit? (Remember thatprofit=revenue-cost.)x=

Answer 1

Since the cost function is

`C(x)=-19x^2+61000x+18324`

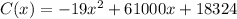
Since the revenue function is

`R(x)=-23x^2+149000x`

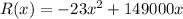
Since the profit function is

`P(x)=R(x)-C(x)`

Then we will subtract C from R

`\begin{gathered} P(x)=-23x^2+149000x-(-19x^2+61000x+18324) \\ P(x)=-23x^2+149000x+19x^2-61000x-18324 \end{gathered}`

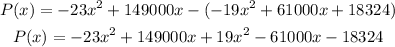
Add the like terms

`\begin{gathered} P(x)=(-23x^2+19x^2)+(149000x-61000x)-18324 \\ P(X)=-4x^2+88000x-18324 \end{gathered}`

Now, we will differentiate P(x) and equate the answer by 0 to find x maximum

`\begin{gathered} P^(\prime)(x)=-4(2)x^(2-1)+88000(1)x^(1-1) \\ P^(\prime)(x)=-8x+88000 \end{gathered}`

Equate P' by 0 to find x

`\begin{gathered} P^(\prime)(x)=0 \\ -8x+88000=0 \end{gathered}`

Subtract 88000 to both sides

`\begin{gathered} -8x+88000-8000=0-88000 \\ -8x=-88000 \end{gathered}`

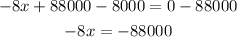
Divide both sides by -8

`\begin{gathered} (-8x)/(-8)=(-88000)/(-8) \\ x=11000 \end{gathered}`

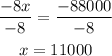
The company should produce 11000 Phones to maximize the profit