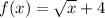Question

Use transformations on the basic function listed below to write a rule

Answer 1

Given:

`f(x)=√(x)`

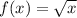
Given the table:

x f(x)

0 0

1 1

4 2

9 3

16 4

Let's write a rule y = f(x) using the table after a transformation of the parent function.

Now, for the graph of the transformed function, we can produce the table, of values:

x g(x)

0 4

1 5

4 6

Now, let's compare both tables:

when x = 0; f(x) = 0, g(x) = f(x) + 4 = 0 + 4 = 4

when x = 1; f(x) = 1, g(x) = f(x) + 4 = 1 + 4 = 5

When x = 4; f(x) = 2, g(x) = f(x) + 4 = 2 + 4 = 6

This means there was a vertical translation 4 units up.

Therefore, the basic function that for the transformation will be: y = f(x) + 4

`f(x)=√(x)+4`

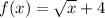
ANSWER:

`f(x)=√(x)+4`