Question

A certain game consists of rolling a single fair die and pays off as follows: $10 for a 6, $7 for a 5, $4 for a 4, and no payoff otherwise,Find the expected winnings for this game.The expected winnings for this game are ?(Round to the nearest hundredth.)Enter your answer in the answer box,

Answer 1

$3.50

Step-by-step explanation:

In a standard die, the total number of possible outcomes = 6.

`\begin{gathered} P(\text{obtaining a 6)=}(1)/(6) \\ P(\text{obtaining a 5)=}(1)/(6) \\ P(\text{obtaining a 4)=}(1)/(6) \\ P(\text{obtaining a 1,2 or 3)=}(3)/(6) \end{gathered}`

To find the expected winnings, multiply each payoff by its probability and sum it up:

`\begin{gathered} \text{Expected Winnings=}(P(\text{others)x}0)+(P(\text{4)x4})+(P(5\text{)x7})+(P(6\text{)x10}) \\ =((3)/(6)*0)+((1)/(6)*4)+((1)/(6)*7)+((1)/(6)*10) \end{gathered}`

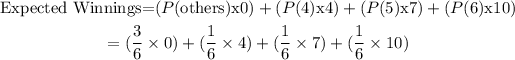
Simplify:

`\begin{gathered} =0+(2)/(3)+(7)/(6)+(10)/(6) \\ \approx\$3.50 \end{gathered}`

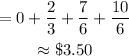
The expected winnings for this game are $3.50 (to the nearest hundredth).