Question

You have 344 grams of a radioactive kind of cobalt. How much will be left after 10 years if its half-life is 5 years?

Answer 1

86 grams

Step-by-step explanation

We have 344 grams of radioactive cobalt.

To find how many years will be left after 10 years if its half life is 5 yrears.

To do this, we apply the formula for exponential decay:

`\begin{gathered} A=A_o\cdot e^{(^(-0.693\cdot t))/(T)} \\ \text{where A}_o=initial\text{ amount} \\ t\text{ = number of years} \\ T=\text{half life} \end{gathered}`

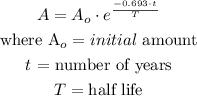
Therefore, we have that:

A - 344 grams

t = 10 years

T = 5 years

`\begin{gathered} A=344\cdot e^{(-0.683\cdot10)/(5)} \\ A=344\cdot e^(-1.386) \\ A=344\cdot0.25 \\ A=86\text{ grams} \end{gathered}`

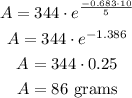
That is the amount that will be left after 10 years.