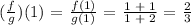Question

Explain how to combine various functions and give examples to show addition, subtraction, multiplication and division of functions with examples

Answer 1

Combining various functions at different operations:

A.) Sum of Two Functions

`(f\text{ + g)(x) = }f(x)\text{ + g(x)}`

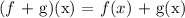
In adding two functions, you add their output of the functions

Example: f(x) = x + 1 and g(x) = x + 2

(f + g)(x) = f(x) + g(x) = (x + 1) + (x + 2) = x + 1 + x + 2 = 2x + 3

(f + g)(1) = f(1) + g(1) = (1 + 1) + (1 + 2) = 2 + 3 = 5

B.) Subtraction of Two Functions

`(f\text{ - g)(x) = f(x) - g(x)}`

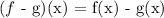
In subtracting two functions, you subtract the output of the functions.

Example: f(x) = x + 1 and g(x) = x + 2

(f - g)(x) = f(x) - g(x) = (x + 1) - (x + 2) = x + 1 - x - 2 = -1

(f - g)(1) = f(x) - g(x) = (1 + 1) - (1 + 2) = 2 - 3 = -1

C.) Multiplication of Two Functions

`\mleft(f\cdot g\mright)\mleft(x\mright)=f\mleft(x\mright)\cdot g\mleft(x\mright)`

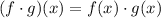
In multiplying two functions, you multiply the output of the functions.

Example: f(x) = x + 1 and g(x) = x + 2

(f * g)(x) = f(x) * g(x) = (x + 1) * (x + 2) = x^2 + 2x + x + 2 = x^2 + 3x + 2

(f * g)(x) = f(x) * g(x) = (1 + 1) * (1 + 2) = 2 * 3 = 6

D.) Division of Two Functions

`\mleft(f/g\mright)\mleft(x\mright)=(f(x))/(g(x))`

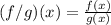
In dividing two functions, you divide the output of the functions.

Example: f(x) = x + 1 and g(x) = x + 2

`((f)/(g))(x)\text{ = }(f(x))/(g(x))\text{ = }\frac{x\text{ + 1}}{x\text{ + 2}}`
`((f)/(g))(1)\text{ = }(f(1))/(g(1))\text{ = }\frac{1\text{ + 1}}{1\text{ + 2}}\text{ = }(2)/(3)`