Question

What is the inverse of g(x)? Is it a function? Explain your reasoning for your response g(x)=x^2-6x+36

Answer 1

`g^(-1)(x)=\pm(\sqrt[]{x-36+6x})`

Step-by-step explanation

`g(x)=x^2-6x+36`

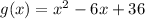
The inverse function returns the original value for which a function gave the output

Step 1

swap x and y and solve for y

so

`\begin{gathered} y=x^2-6x+36 \\ \text{swap x and y } \\ x=y^2-6x+36 \\ \end{gathered}`

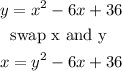
now, isolate y

`\begin{gathered} x=y^2-6x+36 \\ \text{subtract 36 in both sides} \\ x-36=y^2-6x+36-36 \\ x-36=y^2-6x \\ \text{add 6x in both sides} \\ x-36+6x=y^2-6x+6x \\ x-36+6x=y^2 \\ get\text{ the square root in both sides} \\ √(x-36+6x)=√(y^2) \\ \pm(\sqrt[]{x-36+6x})=y \\ y=\pm(\sqrt[]{x-36+6x}) \end{gathered}`

note, there is a negative answer , it is because when gettin the square we get y , so

the answer is

`g^(-1)(x)=\pm(\sqrt[]{x-36+6x})`

I hope this helps you