Question

The width of a rectangle is 8 less than twice its length. If the area of the rectangle is 61 cm^2, what is the length of the diagonal?

Answer 1

The area of a rectangle can be found with the following formula:

`A=lw`

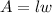
Where "l" is the length and "w" is the widt

In this case, you know that the width of this rectangle is 8 less than twice its length. Then, this can be represented with the following equation:

`w=2l-8`

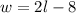
Knowing that:

`A=61cm^2`

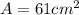
You can substitute values into the formula and simplify:

`\begin{gathered} 61=(l)(2l-8) \\ 61=2l^2-8l \end{gathered}`

Notice that it is a Quadratic Equation, so you can rewrite it in this form:

`2l^2-8l-61=0`

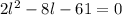
To find "l", use the Quadratic Formula:

`l=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case:

`\begin{gathered} a=2 \\ b=-8 \\ c=-61 \end{gathered}`

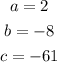
Then, substituting values and evaluating, you get:

`\begin{gathered} l=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(2)(-61)}}{(2)(2)} \\ \\ l_1=\frac{-(-8)+\sqrt[]{(-8)^2-4(2)(-61)}}{(2)(2)}\approx7.87 \\ \\ \\ l_2=\frac{-(-8)+\sqrt[]{(-8)^2-4(2)(-61)}}{(2)(2)}\approx-3.87 \end{gathered}`

Since the length must be positive, you have to choose the positive value. Then:

To find the width, substitute the length into the equation for the width and evaluate:

To understand how to find the length of the diagonal of the rectangle, you need to look at the following image (it is not drawn to scale):

Notice that you have two equal Right triangles. Then, you can apply the Pythagorean Theorem to find the length "d" (in centimeters) of the diagonal (which is the hypotenuse of the Right Triangles):

`c=\sqrt[]{a^2+b^2}`

Where "c" is the hypotenuse of a Right Triangle and "a" and "b" are the legs.

In this case, you can set up that:

Finally, substituting values and evaluating, you get:

Therefore, the answer is: