Question

Which of the following are terms in the sum of the given polynomials?

Answer 1

So we need to perform the following sum:

`P(x)=3x^2-2x^2y+2xy^2+4y^2+xy^2-y^2+2x^2y`

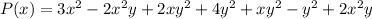
When performing additions and substraction with polynomials is important to remember that like terms can be added separately. Like terms are two or more terms that are multiplied by the same powers of given variables. For example the following are like terms:

`ax^2y\text{ and }bx^2y`

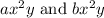
They are like terms because they are numbers a and b multiplied by the same powers of x and y. This powers are common factors of both terms which means that when adding or substracting we can apply the distributive property of the multiplication:

`ax^2y+bx^2y=(a+b)x^2y`

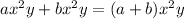
Now we are going to apply this to the sum P(x). First let's list all like terms:

`\begin{gathered} x^2\text{ terms}\colon3x^2 \\ y^2\text{ terms}\colon4y^2,-y^2 \\ x^2y\text{ terms}\colon-2x^2y,2x^2y \\ xy^2\text{ terms}\colon2xy^2,xy^2 \end{gathered}`

Now we take the expression of P(x) and we group the like terms separately:

`\begin{gathered} P(x)=3x^2-2x^2y+2xy^2+4y^2+xy^2-y^2+2x^2y \\ P(x)=3x^2+(4y^2-y^2)+(2x^2y-2x^2y)+(2xy^2+xy^2) \end{gathered}`

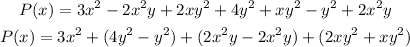
And then we use the distributive property on each pair of terms inside parentheses:

`\begin{gathered} P(x)=3x^2+(4y^2-y^2)+(2x^2y-2x^2y)+(2xy^2+xy^2) \\ P(x)=3x^2+(4-1)y^2+(2-2)x^2y+(2+1)xy^2 \\ P(x)=3x^2+3y^2+3xy^2 \end{gathered}`

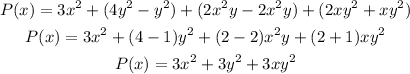
And that's the result of adding all those polynomials. Then the correct options are the second, the fourth and the fifth.