Question

6. A line goes through these two points, (-4,-1) an (-9,-5).A. Find an equation for this line in point slope form.B. Find the equation for this line in slope intercept form. Be sure to show your work.C. If the y-coordinate of a point on this line is 7, what is the x-coordinate of this point?7. Consider the line below.A. Find two points on this linn

Answer 1

A, B) y=4/5x +11/5

C) x=6

6) Since we have those two points, we can find out the slope between them using the slope formula:

`m=(y_2-y_1)/(x_2-x_1)\Rightarrow m=(-5-(-1))/(-9-(-4))=(-4)/(-5)=(4)/(5)`

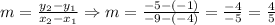
A) In the point-slope form, we can write out the following formula and then plug into that the coordinates the slope found above considering point (-4,-1):

`\begin{gathered} (y-y_1)=m(x-x_1) \\ y-(-1)=(4)/(5)(x+4) \\ y+1=(4)/(5)x+(16)/(5) \\ y=(4)/(5)x+(16)/(5)-1 \\ y=(4)/(5)x+(11)/(5) \end{gathered}`

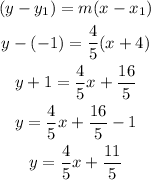
B) The same line described by the slope-intercept formula:

`\begin{gathered} y=(4)/(5)x+b \\ -1=(4)/(5)(-4)+b \\ -1=(-16)/(5)+b \\ -1=-(16)/(5)+b \\ -1+(16)/(5)=b \\ (11)/(5)=b \\ y=(4)/(5)x+(11)/(5) \end{gathered}`

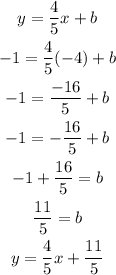
C) Plugging into the function the y-coordinate: 7

`\begin{gathered} y=(4)/(5)x+(11)/(5) \\ 7=(4)/(5)x+(11)/(5) \\ 7-(11)/(5)=(4)/(5)x \\ (24)/(5)=(4)/(5)x\text{ }*5 \\ 24=4x \\ (24)/(4)=(4x)/(4) \\ 6=x \\ x=6 \end{gathered}`

The x-coordinate for y=7 is x= 6.

That's the function y=4/5x +11/5