Step-by-step explanation:
We are given the following information;
25% acid solution + 85% acid solution to derive 80L of 40% acid solution
We shall assign variables to the two different solutions as follows;
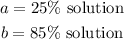
Also we can conclude the following;
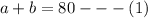
For the amount of acid contents per solution we will have the following;
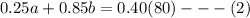
From equation (1), we can make a the subject and we'll have;
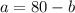
Substitute for the value of a into equation (2);
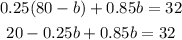
Next we collect like terms and simplify further;
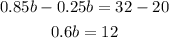
Divide both sides by 0.6;

We can now substitute for b into equation (1);
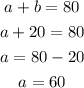
Therefore, we now have;
ANSWER:
For the 25% solution = 60 Liters
For the 85% solution = 20 Liters