Answer:
a. 95%
b. 10.5
c. 1.77
Step-by-step explanation:
To find the probability that x shots are successful from n trials, we will use the following equation for the binomial distribution

In this case, n = 15 free throws, p = 70% which is the probability of success, and we need to calculate the probability that he will make more than 7 throws, so x > 7. Then, the probability is equal to
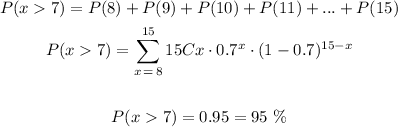
Additionally, the expected value and the standard deviation for a binomial probability are equal to
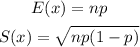
So, replacing n = 15, and p = 0.7, we get:
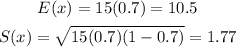
Therefore, the answers are
a. 95%
b. 10.5
c. 1.77