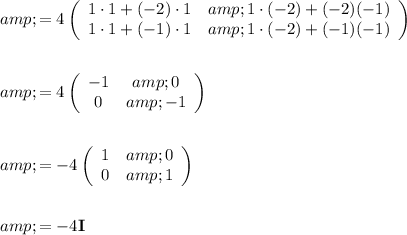Question

Please help with this question!!​

Answer 1

Proof is given below.

Explanation:

Given 2 × 2 matrix:

`\textbf{M}=\left(\begin{array}{cc}2&-2\\1&0\end{array}\right)`

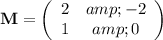
An identity matrix is a square matrix in which the elements on the leading diagonal (starting top left) are all 1 and the remaining elements are zero.

Therefore, the 2 × 2 identity matrix is:

`\textbf{I}=\left(\begin{array}{cc}1&0\\0&1\end{array}\right)`

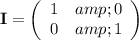
To show that
`\textbf{M}^2=2\textbf{M}-2\textbf{I}` :

`\begin{aligned}\textbf{M}^2&=\textbf{M} \cdot \textbf{M}\\\\&=\left(\begin{array}{cc}2&-2\\1&0\end{array}\right)\left(\begin{array}{cc}2&-2\\1&0\end{array}\right)\\\\&=\left(\begin{array}{cc}2\cdot2+(-2)\cdot1&2\cdot(-2)+(-2)\cdot0\\1\cdot2+0\cdot1&1\cdot(-2)+0\cdot0\end{array}\right)\\\\&=\left(\begin{array}{cc}2&-4\\2&-2\end{array}\right)\\\\&=2\left(\begin{array}{cc}1&-2\\1&-1\end{array}\right)\end{aligned}`

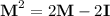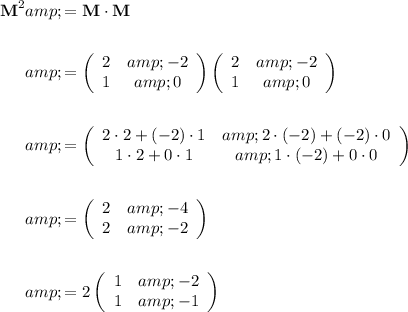
`\begin{aligned} \\\\&=2\left[\left(\begin{array}{cc}2&-2\\1&0\end{array}\right)-\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\right]\\\\&=2[\textbf{M}-\textbf{I}]\\\\&=2\textbf{M}-2\textbf{I}\end{aligned}`

Therefore:

`\begin{aligned}\textbf{M}^4 & =(\textbf{M}^2)^2\\\\&=(2\textbf{M}-2\textbf{I})^2\\\\&=4(\textbf{M}-\textbf{I})^2\\\\&=4\left[\left(\begin{array}{cc}2&-2\\1&0\end{array}\right)-\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\right]^2\\\\&=4\left[\left(\begin{array}{cc}1&-2\\1&-1\end{array}\right)\right]^2\\\\&=4\left(\begin{array}{cc}1&-2\\1&-1\end{array}\right)\left(\begin{array}{cc}1&-2\\1&-1\end{array}\right)\end{aligned}`

`\begin{aligned}&=4\left(\begin{array}{cc}1\cdot1+(-2)\cdot1&1\cdot(-2)+(-2)(-1)\\1\cdot1+(-1)\cdot1&1\cdot(-2)+(-1)(-1)\end{array}\right)\\\\&=4\left(\begin{array}{cc}-1&0\\0&-1\end{array}\right)\\\\&=-4\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\\\\&=-4\textbf{I}\end{aligned}`