Question

Finding solutions in an interval for a trigonometric equation using Pythagorean identities

Answer 1

Write out the equation given

`\cos ^2\theta=2+2\sin \theta`

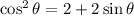
Rearrange the equation, we have

`\cos ^2\mleft(\theta\mright)-2-2\sin \mleft(\theta\mright)=0`

Then recall from trigonometry identies that

`\cos ^2\theta=1-\sin ^2\theta`

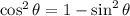
Then substitute into the expression we have

`\begin{gathered} 1-\sin ^2\theta-2-2\sin \theta=0 \\ \text{Then} \\ -\sin ^2\theta-2\sin \theta-1=0 \\ \text{Multiply through by -1, we have } \\ \sin ^2\theta+2\sin \theta+1=0 \end{gathered}`

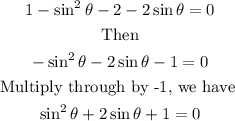
Then

Replace

`\begin{gathered} \sin ^2\theta=p,\text{ we have } \\ p^2+2p+1=0 \end{gathered}`

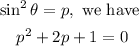
Then, solve by factorization, we have

`\begin{gathered} p^2+p+p+1=0 \\ p(p+1)+1(p+1)=0 \\ (p+1)(p+1)=0 \end{gathered}`

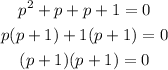
Then we have that

`\begin{gathered} (p+1)^2=0 \\ \text{Then } \\ p+1=0 \\ p=-1 \end{gathered}`

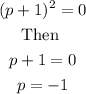
hence, we have that

`\sin \theta=-1`

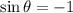
Therefore,

`\theta=\sin ^(-1)(-1)`

Since the interval is

`\begin{gathered} \lbrack0.2\pi) \\ \text{Then } \\ \theta=(3\pi)/(2)\text{ in radians } \end{gathered}`

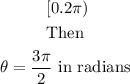
Therefore

Answer: Θ = 3π/2 rads