Question

you will be looking at the choice of buying a bread machine or relying exclusively on store bought bread.The bread machine you are interested in costs $168 with tax.  The ingredients to make one loaf of bread cost $1.50.What is the cost of ingredients for one loaf of bread? (1 pt.) What is your start up cost? (cost of machine) (1 pt.) Write a linear equation, y = mx + b, for the total cost of x loaves of bread. (2 pts.) Graph the equation.  Be sure to locate at least 3 points.  You can do this on paper and insert a picture, or use an online graphing calculator like Desmos and paste a screenshot. (4 pts.) A loaf of bread of similar quality in the store costs $2.50.   This is the rate for a loaf of bread (the slope).  As there is no other cost, your beginning point (y-intercept) is zero.   Write the linear equation y = mx + b for the total cost of x loaves of bread. (2 pts.) Graph the equation on the same graph you used in D.  Be sure to locate at least 3 points.  You can do this on paper and insert a picture, or use an online graphing calculator like Desmos and paste a screenshot. (4 pts.) Estimate the ordered pair where the two lines cross and write it here:   (______, ______) (1 pt.) The x-value where they cross represents the number of loaves it will take to make the costs of the bread machine and buying the bread equal and the y-value represents the cost where they are the same.   Fill in: (2 pts.) It would take _________ loaves at a cost of $_________ for the breadmaker and store bought bread to cost the same.

Answer 1

Given :

The bread machine you are interested in costs $168 with tax.

The ingredients to make one loaf of bread cost $1.50.

A) What is the cost of ingredients for one loaf of bread?

It will be the given value = $1.5

B) What is your start up cost? (cost of machine)

The cost of the machine = $168

C) Write a linear equation, y = mx + b, for the total cost of x loaves of bread.

Let the number of loaves of bread = x

And the total cost = y

so, the equation will be :

`\begin{gathered} m=1.5 \\ b=168 \\ \\ y=1.5x+168 \end{gathered}`

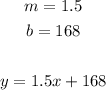
D) Graph the equation. Be sure to locate at least 3 points.

To locate the the points , substitute with 3 value of x and find the corresponding values of y

The graph of the equation will be as shown in the following picture

The 3 points are :

when x = 6 , y = 6 *1.5 + 168 = 177

When x = 10 , y = 10 * 1.5 + 168 = 183

When x = 20 , y = 20 * 1.5 + 168 = 198

So, the points are ( 6,177 ) , ( 10 , 183 ) and ( 20 , 198 ) which are in red colors on the graph

============================

For the second case :

A loaf of bread of similar quality in the store costs $2.50.

And there is no other cost

so, the equation will be :

`\begin{gathered} m=2.5 \\ b=0 \\ \\ y=2.5x \end{gathered}`

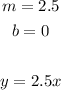
And the graph of the equation will be :

We will graph the two lines on the same graph, it will be as shown in the following figure:

Estimate the ordered pair where the two lines cross:

the red line represents the equation : y = 1.5x + 168

The blue line represents the equation : y = 2.5 x

As shown the order pair where the two lines cross is the point ( 168 , 420 )

So,

It would take _168_ loaves at a cost of $_420_ for the bread maker and store bought bread to cost the same.