We have a polynomial P(x) that is:
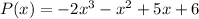
We can calculate the first derivative of P(x). This function P'(x) will tell us the slope of the tangent line to the curve of P(x) for each value of x.
This tangent line has negative slope when P(x) is decreasing and positive slope when P(x) is increasing.
Then,
- when P'(x)<0, P(x) is decreasing.
- when P'(x)>0, P(x) is increasing.
- when P'(x)=0, P(x) is at a exterme point (local minimum of maximum).
We can calculate P'(x) as:
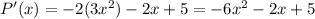
The function P'(x) is concave down, so we can find the roots of P'(x) to see where it changes sign:
![\begin{gathered} x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4\cdot(-6)\cdot5}}{2\cdot(-6)} \\ x=\frac{2\pm\sqrt[]{4+120}}{-12} \\ x=\frac{2\pm\sqrt[]{124}}{-12} \\ x\approx(2\pm11.14)/(-12) \\ x_1=(2-11.14)/(-12)=0.76\approx0.8 \\ x_2=(2+11.14)/(-12)=-1.09\approx-1.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8qnyvzhj5s81q8hq62uquxnyc3d60pqnae.png)
We can evaluate the sign of P'(x) when x<-1.1, for example with P'(2):

Then, we now that P'(x) is positive between x=-1.1 and x=0.8.
In conclusion, P(x) is increasing between x=-1.1 and x=0.8. Outside this interval, P(x) is decreasing.
Answer:
Increasing for x | -1.1 < x < 0.8.
Decreasing for x | x<-1.1 and x>0.8
[Option C]