Question

x = -CD/CD2-40 DC8x2 + 8x = -2Write the quadratic equation in standard form:( a )x2 + ( b )x+ C) = 0Identify the values of a, b, and c.b =Substitute these values into the quadratic formula and simplify:2( )a =C=

Answer 1

So the initial equation is:

`8x^2+8x=-2`

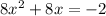
To writte the equation in the standard form we have to make it equal to 0, so we can add 2 in bout sides of the equation:

`\begin{gathered} 8x^2+8x+2=-2+2 \\ 8x^2+8x+2=0 \end{gathered}`

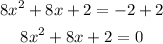
now, (a) is the number thas goes with the x^2, (b) is the number that goes with the x and (c) is the number that is alon, so:

`\begin{gathered} a=8 \\ b=8 \\ c=2 \end{gathered}`

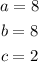
Now we can substitute this numbers in the quadratic equation:

`\begin{gathered} \frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \frac{-8\pm\sqrt[]{8^2-4(8)(2)}}{2(8)} \end{gathered}`

and finally we can simplify the equation:

`\begin{gathered} \frac{-8\pm\sqrt[]{64-64}}{16} \\ (-8)/(16)=(-4)/(8)=(-2)/(4)=-(1)/(2) \end{gathered}`