We are told that the population decreases 9.6% each year. This means that every year, we keep 100-9.6% of the population. That is, we keep 90.4% of the population of the actual population. The equation that represent this, is

Let us number the years referenced to the year in which we have 1000 monkeys. That is, let P0 = 1000. So for year 1 we get
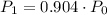
For the year two, we have
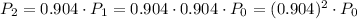
After t years, the population would be
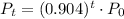
The question is asking what is the value of t if we know that after t years the remaining population is 200 monkeys. So, we have the following equation
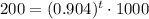
If we divide by 1000 on both sides, we get
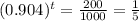
Now, we apply the natural logarithm on both sides, so we get
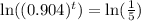
We will apply this properties of logartithms
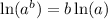
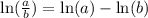
So, we get
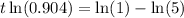
Recall that ln(1)=0. so we get
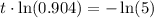
Finally, we divide by ln(0.904) on both sides. So we get
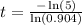
By using a calculator, we get that t=15.9467. Which means that aproximately in 16 years the population of monkeys will be 200.