We have the following sequence:
step 1 has 2 squares
step 2 has 6 squares
step 3 has 12 squares
step 4 has 20 squares
We have to find the number of squares for step n.
The oprtions are:
x^2
x^2+x
2x
x^2+1
If for step 1, we have 2 squares, the option x^2 is discarded as it would predict 1 square.
For step 2 we have 6 squares, so we can test the options:
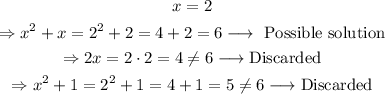
The only option that satisfies step 2 is x^2+x.
We will test it with step 3 and 4:
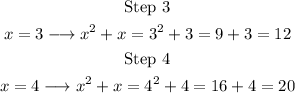
Both are correct, so we can conclude that for step n, the number of squares will be n^2+n
Answer: x^2+x