1 Answer

Emidio Torre · Answer 1 · 2023-05-08T10:06:55+0000

We need to graph the following inequality:

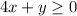
$4x+y\ge0$

First, let's apply the same operations on both sides of the inequality to isolate the variable y on the left side of the inequality. We obtain:

$\begin{gathered} 4x+y-4x\ge0-4x \\ \\ y\ge-4x \end{gathered}$

Now, notice that:

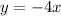
represents a line containing all points with coordinates (x,y) such that y=-4x.

The solution to the inequality includes those points, and also the points for which y is greater than -4x.

Thus, the solution to this inequality consists of all the points on that line (solid line) and the whole region above that line:

Notice that, to graph the solid line, we can choose two points on the line, and then join them. We can use the points:

$\begin{gathered} x=0\Rightarrow y=0\text{ point }(0,0) \\ \\ x=1\Rightarrow y=-4\text{ point }(1,-4) \end{gathered}$

Please log in or register to add a comment.