Question

A marble top bathroom sink has the same shape of a hemispherical (a half-sphere) porcelain bowl with an inside diameter of 11 inches. how much water, in gallons, will the bowl hold? Round to the nearest gallon as needed.

Answer 1

So what we need to do here is find the volume of the bowl in cubic inches and then convert it to gallons. For this purpose is important to recal that:

`1gal=231in^3`

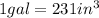
So let's find the volume of the bowl in cubic inches first. The volume of a sphere with a radius r is given by:

`V=(4)/(3)\pi\cdot r^3`

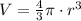
In this case, the bowl is a half-sphere so it has half the volume:

`V=((4)/(3)\pi\cdot r^3)/(2)=(2)/(3)\pi\cdot r^3`

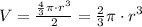
The radius is half the diameter so:

`r=(11in)/(2)=5.5in`

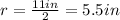
Then the volume of the bowl in cubic inches is:

`V=(2)/(3)\pi\cdot r^3=(2)/(3)\pi\cdot(5.5in)^3=348.45in^3`

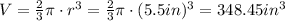
Now using the convertion factor between gallons and cubic inches and the rule of three we get:

`\begin{gathered} 231in^3------1gal \\ 348.45in^3----x \\ x=(348.45in^3\cdot1gal)/(231in^3)=1.5\text{gal} \end{gathered}`

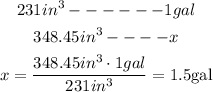
And we need to round our answer to the nearest gallon which means that the answer is 2 gallons.