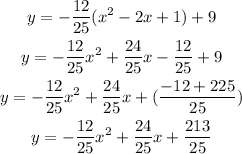Answer:
Vertex form:
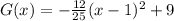
Standard form:
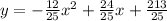
Step-by-step explanation:
A quadratic equation in standard form is generally given as;

where (h, k) is the coordinate of the vertex.
Given the coordinate of the vertex as (1, 9) so we have that h = 1 and k = 9.
Also, given the coordinate of a point on the parabola as (-4, - 3), we have x = -4 and y = -3.
Let's go ahead and substitute the above values to the vertex equation and solve for a as seen below;
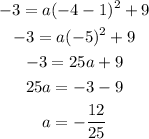
So the vertex form of the quadratic equation can now be written as;
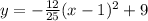
Let's go ahead and expand and simplify the above to have it in standard form;