Solution:
Let x represent a number of calling minutes. According to the problem, we want:
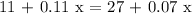
now, putting the similar terms together, we obtain:
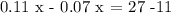
this is equivalent to:
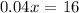
now, solving for x, we get:
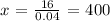
then, the correct answer for the first question is:
400 minutes is the number of minutes the two plans cost the same
now, for the second question, we can replace the above value (400 minutes) into the following equation:
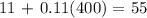
so that, the correct answer for the second question is:
$55 is the cost when the two plans cost the same