Question

Suppose you have $1100 deposited at 4.5% compounded monthly. About long will it take your balance toincrease to $2700? Round your answer to the nearest tenth of a year.years

Answer 1

Recall the formula for compound interest

`\begin{gathered} A=P\Big(1+(r)/(n)\Big)^(nt) \\ \text{where} \\ A\text{ is the accrued amount} \\ P\text{ is the principal amount} \\ r\text{ is the rate as a decimal} \\ n\text{ is the number of compounding period per year} \\ t\text{ is the time in years} \end{gathered}`

Using the formula, rearrange the equation and solve in terms of time t

`\begin{gathered} A=P\Big{(}1+(r)/(n)\Big{)}^(nt) \\ (A)/(P)=\frac{\cancel{P}\Big{(}1+(r)/(n)\Big{)}^(nt)}{\cancel{P}} \\ (A)/(P)=\Big{(}1+(r)/(n)\Big{)}^(nt) \\ \ln \Big((A)/(P)\Big)=\ln \Big(1+(r)/(n)\Big)^(nt) \\ \frac{\ln \Big{(}(A)/(P)\Big{)}}{n\ln \Big{(}1+(r)/(n)\Big{)}}=\frac{nt\ln \Big{(}1+(r)/(n)\Big{)}}{n\ln \Big{(}1+(r)/(n)\Big{)}} \\ t=\frac{\ln \Big{(}(A)/(P)\Big{)}}{n\ln \Big{(}1+(r)/(n)\Big{)}} \end{gathered}`

Substitute the given values and we get

A = $2700, P = $1100, n = 12 (12 months in a year), r = 0.045 (from 4.5%)

`\begin{gathered} t=\frac{\ln\Big{(}(A)/(P)\Big{)}}{n\ln\Big{(}1+(r)/(n)\Big{)}} \\ t=\frac{\ln \Big{(}(2700)/(1100)\Big{)}}{(12)\ln \Big{(}1+(0.045)/(12)\Big{)}} \\ t=19.99 \end{gathered}`

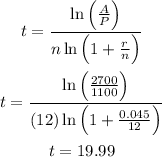
Rounding the answer to the nearest tenth, the time it takes is 20 years.