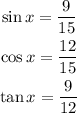Question

Given the triangle below, evalute the sine, cosine and tangent

Answer 1

The sine, cosine and tangent of angle x are;

`\begin{gathered} \sin x=(9)/(15) \\ \cos x=(12)/(15) \\ \tan x=(9)/(12) \end{gathered}`

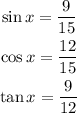
Step-by-step explanation:

Given the triangle in the attached image.

we want to evaluate the sine, cosine and tangent of the angle x;

Recall that;

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \cos \theta=(adjacent)/(hypotenuse) \\ \tan \theta=(opposite)/(adjacent) \end{gathered}`

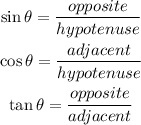
From the given figure;

`\begin{gathered} \text{opposite = 9} \\ \text{adjacent = 12} \\ \text{hypotenuse = 15} \end{gathered}`

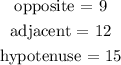
substituting the given values, we have;

`\begin{gathered} \sin x=(opposite)/(hypotenuse)=(9)/(15) \\ \cos x=(adjacent)/(hypotenuse)=(12)/(15) \\ \tan x=(opposite)/(adjacent)=(9)/(12) \end{gathered}`

Therefore, the sine, cosine and tangent of angle x are;

`\begin{gathered} \sin x=(9)/(15) \\ \cos x=(12)/(15) \\ \tan x=(9)/(12) \end{gathered}`