Question

If sin Θ = 5/6, what are the values of cos Θ and tan Θ

Answer 1

Given:

`\sin\theta=(5)/(6)`

Required- the values of cos θ and tan θ.

Step-by-step explanation:

We know that in a right-angled triangle, for any angle θ, the value of sin θ, cos θ, and tan θ is:

`\begin{gathered} \sin\theta=(Opposite)/(Hypotenuse) \\ \\ \cos\theta=(Adjacent)/(Hypotenuse) \\ \\ \tan\theta=\frac{Opposite\text{ }}{Adjacent} \end{gathered}`

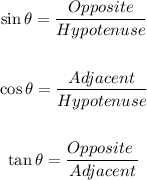
From the given value of sin θ, we get:

`\begin{gathered} Opposite\text{ =5} \\ \\ Hypotenuse\text{ =6} \end{gathered}`

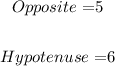
Now, we calculate the value of Adjacent by the Pythagoras theorem as:

`\begin{gathered} (Hypotenuse)^2=(Adjacent)^2+(Opposite)^2 \\ \\ (6)^2=(Adjacent)^2+(5)^2 \\ \\ (Adjacent\text{ \rparen}^2\text{=36-25} \\ \\ Adjacent=√(11) \end{gathered}`

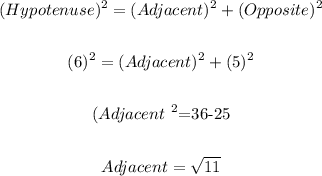
Now, the value of cos θ is:

`\begin{gathered} \cos\theta=(Adjacent)/(Hypotenuse) \\ \\ =(√(11))/(6) \end{gathered}`

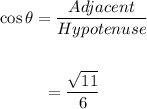
Now, the value of tan θ is:

`\begin{gathered} \tan\theta=(Opposite)/(Adjacent) \\ \\ =(5)/(√(11)) \\ \end{gathered}`

Final answer: The value of cos θ and tan θ is √11/6 and 5/√11 respectively.