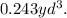To answer this question we will use the following formula to compute the volume of a cube:
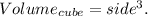
Recall that the volume of a pyramid is one-third the volume of a prism with the same base and height.
From the given diagram we get that the base of the pyramid is the same as the base of the cube, and both figures have the same height, then:
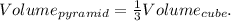
Using the formula for the volume of a cube we get:
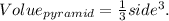
Substituting side=0.9yards we get;
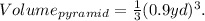
Simplifying the above result we get:
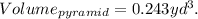
Answer: