Part A. In the given problem a triangle is formed. Since we are required to determine one of its sides given the opposite angle and the other two sides we can use the cosine law:
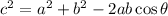
Where:
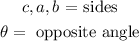
Now, we plug in the values:
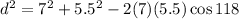
Now, we solve the operations:

Now, we take the square root to both sides:
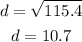
Therefore, the distance between the cars is 10.7 feet.
Part B. We are given the following situation:
We will apply the coside law using the angle "x" as the opposite angle:

Now, we solve the operations:
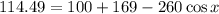
Now, we solve the addition:
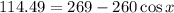
Now, we subtract 269 from both sides:
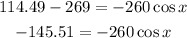
Now, we divide both sides by -260:
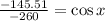
Now, we take the inverse function of the cosine:
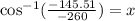
Solving the operations:
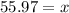
Therefore, angle "x" is 55.97 degrees.
Now, we use angle "y" as the opposite angle. Applying the cosine law we get:
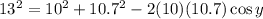
Solving the operations:

Now, we subtract 214.5 from both sides:

Now, we divide both sides by 214
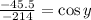
Now, we take the inverse function of the cosine:
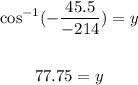
Therefore, angle "y" is 77.72 °
To determine angle "z" we will use the fact that the sum of the interior angles of a triangle always adds up to 180:
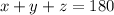
Plugging in the values:
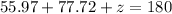
Solving the operations:

Now, we subtract 133.69 from both sides:
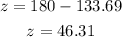
Therefore, angle "z" is 46.31 degrees.