STEP 1: Identify and Set Up
The skywheel can be safely assumed with a circle being divided into sectors by the gondolas and if we're to get the central angle between gondola cars, we're to simply divide total angle by the number of gondola cars.
The we're to also get the radius which will help in our computation of the area of each sector.
STEP 2: Execute
Total angles in a circle = 360 degrees,
Central angle between the gondola cars will be:
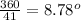
The radius is the length of a straight line drawn from the centre of a circle to any point on its circumference. It is also half the length of the diameter which is the line drawn from a point on the circle to another and passes through the circumference.
Therefore, radius will be gotten as:
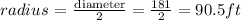
Area of a sector is given as:
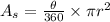
where
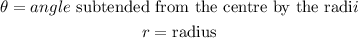
Therefore, our sector's area will be:
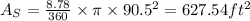
Area of the sector = 627.54 sq ft