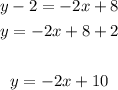Given the points (0,0) and (8,4)
The midpoint will be the point M, which can be calculated as following :
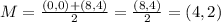
The slope of the line segment with the endpoints (0,0) and (8,4) will be :
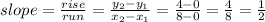
So, the slope of the perpendicular to the given line segment = -2
So, the required line have a slope of -2 and passing through the point ( 4 , 2 )
The slope - point form of the line will be :
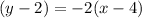
And the general form will be :