We know the centripetal acceleration is given by:
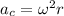
In this case we know that the radius is 7 m and the we want the centripetal acceleration to be 1.85 times that of gravity, then we have:
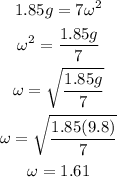
Hence, the angular speed needed is 1.61 rad/s. To determine the revolutions per minute we just need to convert the angular speed we found:

Therefore, at 15.37 rpm the riders will be subjected to 1.85 times the acceleration of gravity.