Question

Determine the equation of the line that passes through the point (-7,-11) and is parallel to the line Y equals 2X -4

Answer 1

a Given:

The equation of line 1 is given as y = 2x-4.

Another line 2 passes parallel through line 1 and through the point (-7,-11).

Step-by-step explanation:

The general equation of the slope-intercept form of a line is,

`y=mx+b\text{ . . . . .(1)}`

By comparing the equation (1) with the equation of line 1,

`m=2`

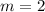
Since line 2 is parallel to line 1, the slope of the two lines will be equal.

To find the equation of line 2:

The equation of line using a slope and a point can be calculated as,

`y-y_1=m(x-x_1)\text{ . . .. .(2)}`

Consider the given point as

`(x_1,y_1)=(-7,-11)`

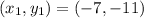
On plugging the obtained values in equation (2),

`\begin{gathered} y-(-11)=2(x-(-7)) \\ y+11=2(x+7) \end{gathered}`

The equation of line 2 in the slope-intercept form will be,

`\begin{gathered} y+11=2x+14 \\ y=2x+14-11 \\ y=2x+3 \end{gathered}`

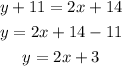
Hence, the equation of line 2 in the slop-intercept form is y = 2x+3.