1 Answer

Jayakrishnan · Answer 1 · 2023-02-13T23:23:25+0000

Given that radioactive substance is reduced by 35 percent in 15 hours.

Let N(0) be the initial quantity and N(15) be the quantity of substance after 15 hours.

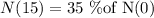
$N(15)=35\text{ \%of N(0)}$

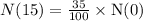
$N(15)=(35)/(100)*\text{N(0)}$

We know that the formula to find the quantity of substance after t hours is

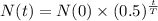
$N(t)=N(0)*(0.5)^{(t)/(T)}$

T is the half-life time.

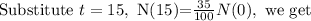
$\text{Substitute }t=15,\text{ N(15)=}(35)/(100)N(0),\text{ we get}$

$(35)/(100)* N(0)=N(0)*(0.5)^{(15)/(T)}$

Cancel out N(0), we get

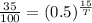
$(35)/(100)=(0.5)^{(15)/(T)}$

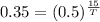
$0.35=(0.5)^{(15)/(T)}$

Taking log on both sides, we get

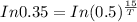
$In0.35=In(0.5)^{(15)/(T)}$
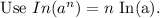
$\text{ Use }In(a^n)=n\text{ In(a).}$

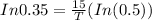
$In0.35=(15)/(T)(In(0.5))^{}$

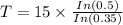
$T=15*(In\mleft(0.5\mright))/(In(0.35))$

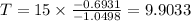
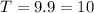
Hence the half-life time is 10 hours.

Please log in or register to add a comment.