Solution
Step 1
A)The domain refers to all values of x for which the function remains defined. Any value of x that makes the function undefined is out of the domain. This can be achieved by factorizing the denominator of the known function to get the values of x that make the function undefined. All other values of x that make the function defined are part of the domain.
Step 2
B)Factorize the denominator
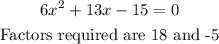
Hence factorizing further we will have
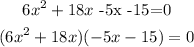
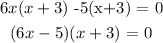
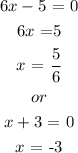
Hence, the domain of the function given is all real values of x except -3 and 5/6