Given,
The mass of the 1st ball, M=5.0 kg
The mass of the 2nd ball. m=3.6 kg
The initial velocity of the 1st ball, u₁=3.2 m/s
The initial velocity of the second ball, u₂=2.7 m/s
The speed of the 1st ball after the collision, v₁=1.5 m/s
From the law of conservation of momentum, the total momentum of a system always remains constant. That is the total momentum of the balls before and after the collision is the same.
Thus,
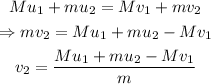
Where v₂ is the velocity of the 3.6 kg ball after the collision.
On substituting the known values,
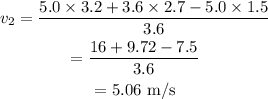
Therefore the velocity of the 3.6 kg ball after the collision is 5.06 m/s